Non-parametric Standard Deviation and Annualized Volatility are two proprietary measures of risk that are included in DazStat.
Premise
The market convention uses the Standard Deviation of the returns as the primary measure of risk – annualized volatility. This is based on the assumption that the returns have a Normal distribution so that Standard Deviation provides a consistent measure of the dispersion of the returns of diverse investments.
As I have repeated many times, there is no guarantee that the returns do indeed have a Normal Distribution, especially if we are looking at active investment returns rather than discrete asset returns. In these cases, using Standard Deviation as the measure of dispersion of returns may mis-estimate the actual dispersion of returns and therefore of risk. Unfortunately, both an over-estimate and an under-estimate will cause problems in portfolio construction and performance evaluation.
This issue lies at the very foundation of CAPM, many optimizers and the ratios used to compare alternative investments. Fortunately, there is a way around the potential for error of assuming a Normal distribution. Even better, it is simple and intuitive!
Non-Parametric Standard Deviation
The dispersion of returns expected within one Standard Deviation of the Mean in a Normal distribution is 68.27% of all returns. That is the dispersion that we are assuming, but unsure of, when we use Standard Deviation as the basis for our definition of ‘risk’.
Rather than making an assumption, let’s just make a calculation! Measure the absolute distance of all the returns from the mean then rank them. Take the 68.27 percentile value and that is the actual range of dispersion, and that Standard Deviation is trying to measure. That is the Non-parametric Standard Deviation – it makes no assumptions about the nature and parameterization of the distribution of returns. It is not, of course, a Standard Deviation, which is one of the two parameters that define Normal distributions. It is the direct measure of dispersion that Standard Deviation is assumed to be measuring but may not be! If the distribution is Normal, then the Non-parametric Standard Deviation and Standard Deviation will be the same so that no harm is done.
If the distribution is not normal it may be that the distribution, unlike a Normal distribution, is not symmetrical either. The Non-parametric Standard Deviation measures the boundary point that includes 68.27% of the returns, but they may be unequally weighted to the upside or downside. The DazStat function provides two more measures of Upside Dispersion and Downside Dispersion, each of which contains 34.13% of the sample. These two values mark the actual 68.27% range of dispersion in the returns.
Non-Parametric Annualized Volatility
Following the market convention, we can take the Non-parametric Standard Deviation and scale it to an annualized rate using the square root of the number of return periods in a year.
Example
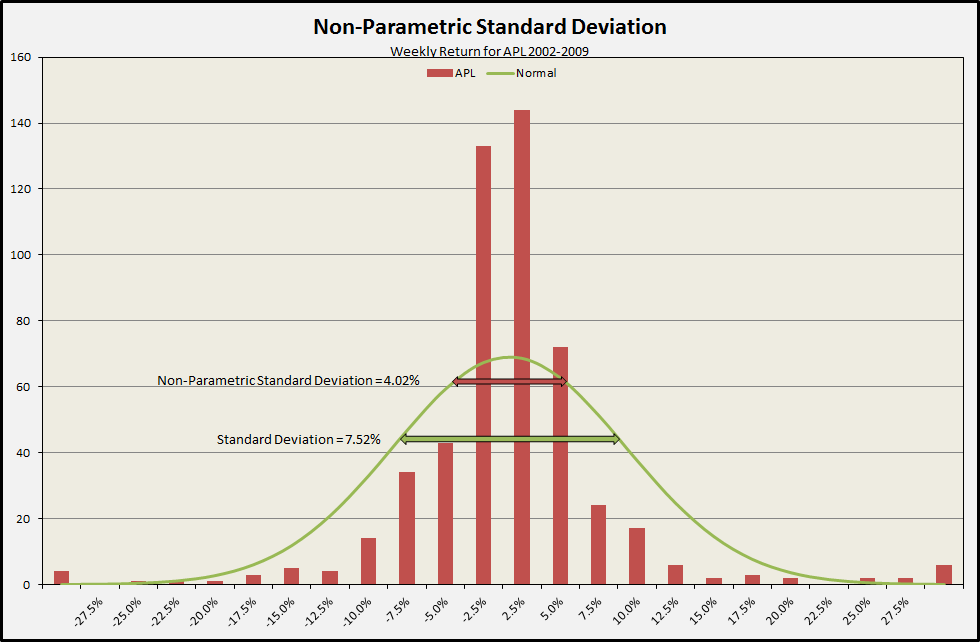
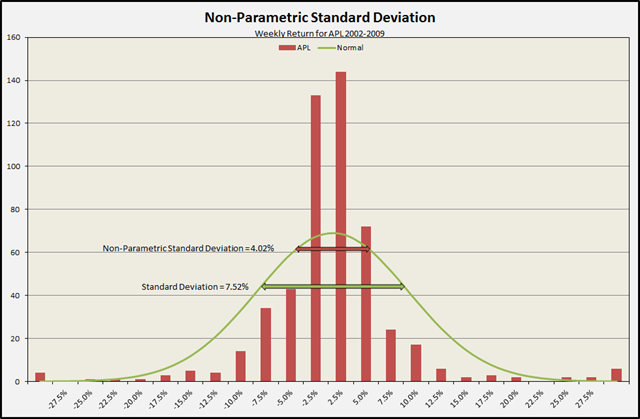
Here is a simple example from the weekly returns of the MLP Atlas Pipeline Partners (APL) from 2002 through 2009. It has had some dramatic volatility: mean return of 0.42%, maximum return of 52.14% and a minimum return of –53.53%. The Standard Deviation is 7.52% (for a whopping 54.21% annualized). Look at that green curve – that is the Normal distribution fit to the returns! It over-estimates the number of returns over the middle range of the distribution. That is exactly where the Standard Deviation is measured. In fact, 68.27% of the weekly returns of APL fall within +/- 4.02% and not 7.52%. That is the Non-parametric Standard Deviation that is measuring the actual distribution of observed returns rather than assuming a Normal distribution of returns. A Non-parametric Standard Deviation of 4.02% (28.97% annualized) is the real number we are looking for.
Here are some values from the DazStat Examples workbook.
Some of the Annualized Volatility (Normal assumption) estimates are significantly different from the Non-parametric Annualized Volatility actual dispersion. In general, we expect that Non-parametric Standard Deviation will be lower than the Normal Standard Deviation – less volatility within the 68.27% range. That will throw-off all the risk-adjusted performance measures that use Standard Deviation for risk – the ubiquitous Sharpe Ratio included. Caveat Investor.